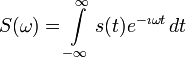
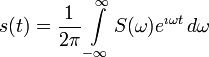
Fourierova transformace 1D případ

Stručný popis

Fourierova transformace slouží k převodu signálu v časové (prostorové) doméně, do domény frekvenční. Jedná se vlastně o rozklad časového průběhu do „sumy“ průběhů harmonických. Tyto harmonické různých frekvencí tvoří bázi nového prostoru (závisle proměnná). Základním signálem ve frekvenční doméně je harmonický signál – sinus a cosinus. Pro každou frekvenci se hledá její nejlepší umístění v signálu. Toto je reprezentováno velikostí – amplitudou, a fázovým posunem (popřípadě kombinací sinu a cosinu). Výsledkem shody pro danou frekvenci je komplexní číslo.

FT je výhodná pro práci se signálem, zejména pro různé typy filtrací. Je omezena na lineární operace. Je výhodná pro stacionární signály (shoda pro danou frekvence se provádí na celém intervalu a musí být proto přítomná po celou dobu trvání (v časové oblasti)). V případě, že signál o dané frekvenci je v celkovém signálu obsažen jen z části (v určitém časovém podintervalu) – není z FT možná jeho lokalizace v originálu.

Periodický signál – signál, který se po určitém (pevně daném) čase opakuje

Signál, který není na celém intervalu – například sinusový signál, který se vyskytuje pouze uprostřed intervalu.

vzorce a vlastnosti (věty o posunutí ...) spojitá a diskrétní, přímá a zpětná

(Pozn. / omluva: - vzorce pocházejí z různých zdrojů a nemají tedy jednotnou formu zápisu ani pojmenování proměnných)

Obrázek znázorňuje původní signál a jeho obraz ve FT (Obraz v FT má dvě složky – amplitudu a fázi). Máme-li signál v časové (prostorové) doméně, potom pomocí (přímé) FT získáme jeho obraz v doméně frekvenční. Z frekvenční domény pomocí Inverzní FT (IFT) získáme signál v doméně časové. Jelikož je FT (IFT) lineární a bezztrátová transformace, musí se takto vytořený signál shodovat se signálem původním Signal = IFT(FT(Signal)). První hodnota (v nule) odpovídá stejnosměrné složce signálu, následující jsou pro zvyšující se frekvence (vpravo je frekvence nejvyšš).

Pro spojitou FT je přímá transformace                             zpětná (inverzní) transformace

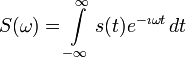
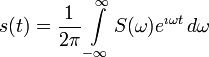
Je uvedena nesymetrická varianta.  Část  může někdy být v přímé transformaci a někdy je “rozpůlena” – je v odmocnině u přímé i zpětné transformace (symetrická verze). Při cyklu přímá, zpětná nedochází ke ztrátě. V prostorové doméně je proměnnou čas, ve frekvenční doméně w.

                                spektrum je komplexní číslo. Signál v časové oblasti předpokládáme reálný.

Pro diskrétní signály byla odvozena diskrétní FT  opět přímá a zpětná varianta (hovoříme o vzorcích, nebo krocích signálu)

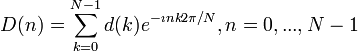
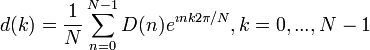
k jsou indexy (kroky) v prostorové doméně
n jsou indexy ve frekvenční doméně
N je počet vzorků
d signál
D spektrum

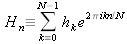
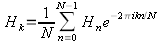jiný zápis

Základní vlastnosti FT jsou:

- je asociativní – nezáleží na pořadí provádění operací. Tato vlastnost nám dává možnost „seskupit“ lineární filtry aplikované postupně za sebou do jediného přenosu a tím ušetřit výpočetní náročnost, protože využívaný filtr se vypočítá pouze jednou a potom se s ním nadále pracuje jako s jediným celkem - ( F1xF2xF3xF4 ) x S = ( Fc ) x S

- je komutativní – nezávisí na pořadí argumentů. A je tedy možné ve výpočtech zaměňovat signály (Signál <-> Filtr).

- vlastnost změna měřítka – „resampling“ , může sloužit k převzorkování signálu – změně měřítka, nebo „dopočítání“ chybějících bodů

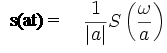
- věta o posunutí. Posuneme-li vstupní signál (s cyklickým přesahem v rámci periody), potom výsledný obraz má stejnou amplitudu, ale „posunutou“ fázi

Další výhodou převodu do FT je menší výpočetní náročnost korelace/konvoluce (Při hodnocení nutné ovšem započítat režii pro převody do a z FT, v horším případě pro více snímků a filtrů). Konvoluce (násobení přes všechny pixely snímku a přes celou plochu filtru) se mění na násobení odpovídajících si prvků spektra (stejné frekvence).

Významnou vlastností, která se využívá při různých (ztrátových) kompresních algoritmech je to, že většinou platí, že vyšší frekvence mají nižší hodnotu (energii) a jejich odstranění tedy způsobí menší ztráty (tato vlastnost je patrná již z uvedených obrázků, kdy amplituda pro vyšší frekvence klesá).

Frekvence udává počet period, které se vejdou do časové jednotky.

Perioda je časový úsek, po kterém se signál začne opakovat.

Kruhová frekvence w = 2 Pi f = 2 Pi / T [rad/s ; Hz ; s]

Ve frekvenční oblasti většinou zobrazujeme závislost amplitudy a fáze na (kruhové) frekvenci. Zobrazení v komplexní rovině (známé z regulace) nebývá ve zpracování obrazu zvykem. Z důvodu nesouměřitelnosti signálů (kdy například ss složka je výrazně vyšší než složky ostatní) se často používá převod hodnot amplitudy do logaritmické stupnice

Ukázky

Vytvoření obdélníku z 1, 2, 3, 7 harmonických. FT obdélníků – spektrum klesá směrem k vyšším frekvencím – využití ve ztrátových transformacích (vyšší frekvence -> nižší amplituda)

snímek ukazuje kvalitu vytvořeného obdélníkového signálu, je-li použito prvních 4, 10, 25 členů

Vytvoření lineárního nárůstu z 1,2,4,8 harmonických („klidné“ části kvalitnější než přechody)

lineární nárůst a jeho aproximace při použití 4, 10, 25 členů. Je vidět, že k největší chybě dochází na prudké změně signálu (nezapomínejme, že dochází k periodickému doplnění signálu za okraje). Nejhorší výsledky při použití FT jsou právě při použití rychle se měnících signálů (záznamy seismografů, pravoúhlý signál …). Je to i vlastnost toho, že prudké změny jsou realizovány vysokými frekvencemi, které zde nejsou využity.

Nevýhodou „rychlých“ přechodů je i to, že jsou to lokální jevy, zatímco (jak bylo uvedeno výše) FT předpokládá, že se dané frekvence projevují (nejlépe rovnoměrně) na celém intervalu. Pro vyjádření pomalých dějů stačí menší množství vzorků, pro přesnější vyjádření rychlých dějů, potřebujeme složek více.

Z daných vlastností je zřejmé, že pro kvalitní popis musíme počítat se všemi frekvencemi, které jsou zastoupeny – jejich vypuštění vede ke změně tvaru signálu. Čím více frekvencí se použije, tím lépe jsou vyjádřeny konstantní úseky a  přechody. V okolí přechodů dochází při vypuštění části spektra ke kmitání (nízké frekvence popíší základní tvar a vysoké ho upřesňují).

Pojem sudá a lichá funkce
sudá funkce je symetrická podle osy y. Je vyjádřena pouze cosinusovými členy.
Lichá funkce je symetrická podle osy y ale má opačné znaménko.
Změnu lze realizovat posunutím. kdy lze z obdélníků udělat lichou/sudou je-li správně periodická – musí být periodická. Periodické rozšíření se používá proto, že periodická funkce má diskrétní spektrum = předpoklad periodické rozšíření (přesah při filtraci)
Podobně se chová i lineárně narůstající signál – amplitudová část spektra je stejná, při posunu se mění pouze fáze.

Změnu liché na sudou lze realizovat posunutím. kdy lze z obdélníků udělat lichou/sudou je-li správně periodická – musí být periodická. Periodické rozšíření se používá proto, že periodická funkce má diskrétní spektrum = předpoklad periodické rozšíření (přesah při filtraci)

jak se převádí dané typy signálu:
- spojitý, neperiodický -> spojitý
- spojitý, periodický -> nespojitý (diskrétní)
- diskrétní, neperiodický -> spojitý
- diskrétní, periodický -> nespojitý

zpracování signálu – konvoluce, korelace, autokorelace

Výhodou výpočtů ve frekvenční oblasti je snadnost základní operace, která popisuje činnost filtrů – konvoluce – a s ní související korelace a autokorelace. Obtížně počítatelná konvoluce v časové oblasti se mění na násobení (respektive dělení) v oblasti frekvenční. Konvoluce je operace mezi signálem a „popisem“ filtru. U signálů, které jsou periodicky rozšířeny musíme brát v úvahu „přesahy“ na okrajích zpracovávaných intervalů.

Při výpočtech je nutné brát do úvahy časovou náročnost výpočtu v prostorové doméně a tuto srovnávat s řetězcem převod->výpočet ve frekvenční oblasti->zpětný převod. Převody jsou „zátěží“ (nutnou režií) při výpočtech ve frekvenční oblasti. Tuto režií lze snížit, pokud si často používané filtry předpočítáme. Čas nutný pro převod lze zkrátit využitím některých vlastností FT (plynoucích z dané délky (FFT) nebo z toho, že vstupní data jsou reálná). Rozdíly ve výpočetní náročnosti se projevují především při použití více jednoduchých filtrů za sebou nebo při použití filtrů se složitějším tvarem (Gauss, Canny, Spacek ...), které v prostorové oblasti nelze kvalitně optimalizovat. Některé operace (inversní filtrace ...) jsou v časové oblasti nemyslitelné.

FFT – přesah, doplňování nulou

Nevýhodou FT je její výpočetní (především časová) náročnost. Doba nutná pro převod do a z frekvenční domény je díky vnořeným cyklům nutným pro výpočet velice velká a pro většinu výpočtů s rozsáhlejšími daty proto nepoužitelná. Tuto výpočetní náročnost odstranil algoritmus (ve skutečnosti je jich více, díky různým způsobům realizace, ale princip je stejný) rychlé FT (FastFT, FFT). Díky principu optimalizace výpočtů (něco jako „vytýkání“) se výpočetní náročnost snižuje z náročnosti NxN na Nxlog2 N.

To vše se děje díky pevné délce, která pro tyto optimalizace musí být mocninou 2. Výsledné převody FFT a IFFT jsou podstatně rychlejší než FT a IFT (které však mohou být prováděny nad signálem obecné délky).

Další vlastnost (která se mlčky předpokládá) je, že původní signál je periodický (jelikož jeho spektrum je diskrétní). Periodicity dosáhneme tak, že pracujeme s vybraným intervalem a mlčky předpokládáme, že mimo tento interval se signál v něm obsažený periodicky opakuje. Tato vlastnost se může nepříznivě projevi při filtraci, kdy při použití „širších“ filtrů dochází k tomu, že výsledný signál u „okraje“ je ovlivněn signálem z „druhé strany“, který je díky periodickému rozšíření signálem sousedním a filtr do něj zasahuje při výpočtech. Tento jev je možné odstranit tím, že signál vhodně doplníme (na okraji z jedné nebo obou stran). Pokud chceme dostat přesný signál, doplňujeme nuly. Jelikož toto doplnění může způsobit „strmou“hranu v signálu, použíje se někdy k doplnění pozvolnější přechod, se kterým si následně transformace lépe poradí.

programování

Při programování, nebo realizaci se využívá již zmíněných vlastností, nebo se používá jiných HW prostředků. Při programování je možné naprogramovat algoritmy FT ale běžnější jsou DFT nebo FFT. Existuje celá řada implementací, která se řeší přístupem k optimalizacím výpočtů daných algoritmů. Existují i možnosti implementace na bázi DSP, GPU či hradlových polí (paralelní výpočty menších rozměrů) a to jak pro celkové výpočty tak i pro výpočty částečné. Například je možné předpočítat FT optimalizovaně v HW pro základní bloky o délce 8 (16,32 ...) a ty následně dopočítat standardně.

Základního zrychlení se dosahuje implementací FFT, za které je nutné „zaplatit“ definovanou délkou signálu (mocnina dvou). Dalšího zrychlení je možné dosáhnout předpočítáním hodnot které se opakují (například tabulka sinů a cosinů, předpočítání spekter filtrů, tvarů a objektů, které se nejčastěji používají...). Dalšího zrychlení je možné dosáhnout společným počítáním více signálů, nebo lepší implementací algoritmů. Při výpočtech se využívá podobnosti – duplicity – ve výpočtech (něco jako vytýkání u klasických výpočtů) ke snížení výpočetní náročnosti. A dále se využívají rekurzívní algoritmy (půlení řady).

Je možné využít vlastností a symetrií mezi prostorovými a frekvenčními prostory, při řešení reálných, imaginárních, lichých či sudých funkcí, kdy je možné zjistit zákonitosti a ty využít k optimalizaci výpočtů. Jelikož je vstupní signál reálný a výpočty jsou koncipovány pro komplexní čísla, je možné počítat dvě řady zaráz tak, že jedna je v komplexní složce a druhá v reálné. Výhodou tohoto algoritmu je snadné oddělení příslušných spekter z výsledného spektra. Je též možné počítat signál jako dva poloviční (umístěné jako dva z minulého příkladu).

Možná zrychlení tedy pramení z vlastností (lichá, sudá, reálná řada) FT tak, že vstupem jsou většinou reálné řady. Je-li jedna řada vložena na místo reálných koeficientů a druhá řada na místo imaginární složky, potom lze počítat společně a výsledky lze rozdělit na obrazy jednotlivých složek. Pro převod jedné řady lze volit i její rozpůlení do reálné a imaginární složky – opět existují vzorce na přepočet do správného spektra (inverzní úprava je náročnější ale je možná)

Klasická DFT je schopná pracovat s libovolně dlouhým signálem, ale její výpočetní náročnost DFT je velice vysoká (NxN komplexních operací). Rychlá FT (FFT) pracuje se signály délky mocniny dvou a její výpočetní náročnost je Nxlog2 N

Na úvod algoritmu FFT je nutné „přeskládat“ koeficienty a teprve potom spustit vlastní algoritmus výpočtu FFT. První a poslední koeficient FT jsou nezávislé a reálné, proto se poslední často vrací jako imaginární složka prvního

Existuje několik způsobů výpočtů (vzorečků, algoritmizace) – reprezentace se mírně mění na základě zvolené metody optimalizace výpočtu

filtry, tvorba a využití (filtrace)

K filtraci slouží klasický konvolutorní/korelační princip – tyto filtry lze s výhodou převádět do frekvenční oblasti (díky jejich linearitě). Nelineární filtry (medián, prostorově závislé úpravy …) se realizují obtížně.

Filtry pro zpracování signálů, které není nutné provádět v reálném čase (což v image procesingu lze), mohou být „symetrické“ kolem středu. Na rozdíl od zpracování časových signálů, kdy není možné pracovat se vzorky, které teprve přijdou, je zde možné použít kompletní okolí pro výpočet výsledné hodnoty. V tomto signálu (obrázku) známe celé okolí a tedy můžeme mít filtr symetrický k místu, pro které výsledek počítáme. Výhodou tedy je, že lze udělat i derivaci v daném místě (jsou známy hodnoty na obou stranách). Pokud zpracováváme signály v reálném čase, můžeme pro výpočet použít pouze signály současný a minulé.

„Jednoduché“(hranové) filtry bývá lepší realizovat v prostorové doméně (díky možnosti optimalizace jejich výpočtu a časové náročnosti převodu FT a IFT). Složitější a složené filtry je výhodnější realizovat ve frekvenční oblasti.

Nezapomínejme na periodické doplnění signálů při FT. To znamená, že  filtr na okrajích zasahuje „na druhou stranu“. Tyto přesahy musíme vyřešit – budťo rozšířením signálu o „prázdné“ kraje, nebo vypuštěním „přesahů“ z výsledku. V případě, že signál doplňujeme na krajích, neměli bychom to dělat „ostře“. S tímto souvisí i volba velikosti (rozměr) signálu pro výpočet, který musí být mocninou dvou. Musíme tento rozměr volit tak, aby byl dostatečně velký pro výpočet, ale zároveň aby nebyl zbytečně velký, protože by docházelo ke zbytečným výpočtům. Řešením také je provést výpočet a „znehodnocené“ krajní výsledky „zahodit“.

Z obrazu  jednotkového skoku je patrné, že je jím sinc, který v sobě obsahuje „celé“ (=široké) spektrum.  Proto jsou filtry nejčastěji aplikované v prostorové doméně (s ostrými hranami) v doméně frekvenční nevhodné (obsahují vždy široké spektrum a vyšší frekvence mají vyšší váhu než frekvence předchozí – není to frekvenční propust).  Filtry ve frekvenční oblasti by měly omezovat frekvenční  spektrum tak aby „ořezávaly“ frekvence „větší než“. Opět se nedoporučuje ostrý skok ve frekvenční oblasti (z důvodu, že zpětná transformace je opět sinc a tedy filtr by bral široké okolí). Přechod z „propustné“ do „nepropustné“ části frekvencí je lepší volit plynulý. Často se používá signál, který je variací na gaussovu křivku (gauss, laplace, spacek, canny … kdy inverzní funkce je podobná funkci originální). Popřípadě filtry generované na základě čebyševa …

Návrh těchto filtrů umožňuje splnit požadavky na odstranění šumu, kvalitní umístění hrany i odstranit vícenásobné odezvy (maxima ve výstupu filtru) v oblasti hrany.

Filtry ve FT jsou nejčastěji realizovány na bázi podobnosti s gaussovou křivkou.  Tyto filtry jsou „rozmazávací“.  Gaussovou křivkou se aproximuje také „rozložení“ paprsku na optice (PSF). Nebo-li předpokládáme, že se procházející kvalitní (ostře ohraničený) paprsek při průchodu optickou soustavou „rozostřuje“ vlivem prostředí.  Pro modelování tohoto jevu se používá gaussova křivka. Jedná se vlastně o „filtr“,  který je  nechtěný, parazitní a který je tvořen prostředím, kterým pořizujeme snímky. V přesnějších modelech je nutné s jeho vlivem počítat. K tomu musíme mít možnost stanovit jeho model a identifikovat  velikost  jeho parametrů. Na základě stanovení modelu a parametrů můžeme následně provádět i zpětné korekce obrazu.

Filtry vhodné pro hrany potom odvozujeme od těchto filtrů jako jejich derivaci. Z náhledu je zřejmé, že se u těchto hranových filtrů nejedná o filtry vysokofrekvenční jak by se dalo očekávat u hranových detektorů,  ale o filtry středněfrekvenční. Použití středněfrekvenčních filtrů je kompromisem mezi zvýrazněním hrany (potlačením ss složek) a eliminací šumu (vf složek). Při použití pouze vysokofrekvenční složky by došlo ke zvýraznění signálů s vysokými frekvencemi, kterými je (bohužel) často aditivní šum připojený ke snímku. Jelikož požadujeme u filtrů invariantnost vůči šumu, je nutné vysoké frekvence potlačit i za cenu toho, že maxima hranového filtru nebudou kvalitní (ostrá, výrazná).

V inversní a wienerevské filtraci můžeme modelů filtrů, které reprezentují zkreslení, využít i ke zpětnému obnovení „původního“ signálu. Známe-li model zkreslení (rozostření a to jak nezaostřením tak například rozmazání pohybem detektoru), můžeme ho použít k „opravení“ signálu.

Je možné odstranit i periodické rušení, které je superponováno na užitečný signál. V závislosti na poměru rušení k užitečnému signálu je možné buď odstranit (vymazat) příslušnou frekvenci, nebo lépe použít medián okolí (nulování nelze použít v případě, že šum je srovnatelný (či menší) se signálem, kdy odstraněním „špatné“ i „dobré“ složky na dané frekvenci vznikne „inverzní“ chyba) .

last modification 2009-09-16