Fourierova transformace ve 2D

Stručný popis

Fourierova transformace v dvourozměrném prostoru (2D) je rozšířením základní jednorozměrné FT na dvourozměrný signál. I ve 2D je FT matematická metoda/operace, která dovoluje úspěšně analyzovat signály, v našem případě obrazy (2D signály). U FT se jedná o vyjádření funkce, která popisuje obraz v jiných proměnných pomocí integrální transformace a převádí jej na součet sinusových signálů pomocí vhodných frekvencí a amplitud. „Klasická“ jednorozměrná báze FT je založena na funkci exp (amplituda/sinus/cosinus/ fáze), kdy hledáme příspěvek dané frekvence (diskrétní) k signálu. Výsledek odpovídá polohou frekvenci, vlastní hodnota potom amplitudě a fázi (sinus+cosinus).

U dvourozměrné varianty FT je základem prostorová („dvourozměrná“) frekvence, která se dá popsat jako „natočený vlnitý plech“ - sinusový průběh „natažený“ do plochy (ve směru kolmém na časovou osu i osu hodnot). Vzdálenost výsledných hodnot od počátku frekvenční roviny udává narůstající frekvenci. Směr vůči počátku udává natočení vln, tj směr maxim. Vlastní hodnota udává amplitudu a fázi. Výsledkem prvků „plochy“ je spektrum prostorových frekvencí, které tvoří bázi. Výsledný prostorový obraz je součtem příspěvku všech frekvencí (a směrů) s příslušnou váhou (amplitudou). Vlastní vyjádření obrazů jsou komplexně sdružené body (amplituda+fáze).

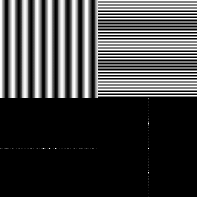
Pojem prostorové frekvence – základem je „sinusovka“ v 2D je to „vlnitý plech“=“natažená sinusovka“. tento má frekvenci, posun a natočení. výsledný signál je opět superpozice. Složení v prostorové doméně několika sinusovek. Frekvence – symetricky umístěné body. Vzdálenost udává frekvenci, komplexnost udává fázi. velikost udává amplitudu. Směr „plechů“ je realizován v závislosti na „směru“ dvojice bodů. Na snímcích výše jsou dvě prostorové předlohy a pod nimi jejich spektra. Je patrné, že určují směr a periodu – hustší síť má obrazy (první harmonické) dále od středu

Využití FT v 2D je podobné jako v 1D. Fourierova transformace (FT) umožnuje provádět frekvenční filtraci, tedy obecně aplikovat filtry na signál. Můžeme „rozmazávat“, „hranovat“, odstraňovat ze signálu části s různými frekvencemi. Operace ve frekvenční oblasti mohou upravovat obrazy takovým způsobem, aby např. došlo ke zvýraznení hran, snížení úrovně šumu, k odstranění „proužkování“ či ke zvýraznění některých struktur v obraze. Nejčastěji se používá pro detekci hran a segmentaci obrazu, úpravu kvality obrazu, rekonstrukci obrazu, kompresi obrazu (formát JPG), detekci objektů atd.

vzorce a vlastnosti

Vzorce spojité 2D

Základem fouriérovy transformace je převod mezi časovou x(t) a frekvenční X(f) oblastí:

x(t) ó X(f)

kde, t je časová (prostorová oblast)

f je frekvenční oblast

Pro přímou spojitou FT je základní definice:

Pro zpětnou spojitou FT je základní definice:

Na x(t) jsou kladeny požadavky, aby byla po částech spojitá a integrovatelná: .

Diskrétní fouriérova transformace 2D

Pro digitální obrazy fouriérova transformace vždy existuje, protože digitální obrazy jsou omezené a mají konečný počet nespojitostí. Fourierovu transformaci můžeme zapsat v maticové podobě, Nechť Φ_JJje transformační matice rozměru J x J a j je imaginární jednotka:

k,l = 0,1,…,J-1

Diskrétní fouriérova transformace je definována dle vztahu F = P f Q, když přiřadíme P = Φ_MM, Q = Φ_NN, a to v maticovém zápisu

F = Φ_MMf Φ_NN

nebo lze vyjádřit pomocí zápisu se sumami

u = 0,1,…,M-1

v = 0,1,…,N-1

Inverzní transformančí matice je:

a inverzní Fourierovu transformaci můžeme zapsat jako :

S ohledem na rychlou implementaci lze rovnice přepsat pomocí separace proměnných jako:

u = 0,1,…,M-1

v = 0,1,…,N-1

Výraz v hranatých závorkách odpovídá jenorozměrné DFT m-té řádky obrazu a lze ho vypočítat standartní rychlou Fouriérovou transformací (FFT, za předpokladu N = 2^k). Každý řádek je nahrazen svou DFT a potom je vypočtena jednorozměrná DFT každého sloupce.

Obraz obdélníku a vliv omezení spektra na rekonstrukci

Pro základní demonstraci zvolme obdélník a jeho obraz ve FT. Všimněte si dvou hlavních směrů spektra v transformaci, které respektují natočení obdélníku. Ve středu frekvenční oblasti je stejnosměrná složka, která udává ss posunutí (v hodnotách, to znamená, že udává střední „výška“ obrazu). Směrem ke kraji se zvětšují frekvence, a je zde patrné i snižování amplitudy pro tyto vyšší frekvence (v nižších frekvencích je více „energie“). Nižší frekvence respektují/vytvářejí základní tvar, vyšší frekvence tvar dokreslují - popisují ostré přechody (hrany). Jednotlivé frekvence se doplňují/skládají - žádná z obsažených frekvencí (pro běžný snímek) není „zázračná“ = nepostihuje zásadním způsobem prostorovou scénu.

obrázek 2D pulzu (tj do 2D natažený obdélníkový průběh) a jeho obraz. Je zde vidět, že FT je pouze v jednom směru ve kterém popusuje hrany (obdélník). Ve druhém směru ve spektru „nic není“, protože v tomto směru je signál konstantní, vyskytují se zde pouze ss složky (všimněte si separace proměnných ve vzorci – každá proměnná se dá počítat zvlášť)

ukázka různě natočených sinusových signálů s různými frekvencemi a jejich spektra.

ukázka principu superpozice, kdy výsledný obraz v prostorové i frekvenční doméně jsou součtem odpovídajících složek (součet v prostorové oblasti a převod dá totéž co převod a součet = linearita).

Pojem prostorové frekvence – základem je sinusovka v 1D, v 2D je to „vlnitý plech“=“natažená sinusovka“. tento má frekvenci, posun a natočení. výsledný signál je opět superpozice. Složení v prostorové doméně několika sinusovek. Frekvence – symetricky umístěné body. Vzdálenost udává frekvenci, komplexnost udává fázi. velikost udává amplitudu. Směr plechů v závislosti na „směru“ dvojice bodů.

Pro vyjádření 2D signálů se používá 2D frekvenční spektrum. Toto spektrum je symetrické podle počátku. Jedná se o sinusový průběh v jednom směru a konstantní hodnotu ve směru kolmém. Směr pruhů udává poloha ve frekvenční rovině. Vlastní hodnoty potom fázi a amplitudu pruhů.

Čím jsou body dále od středu tím je frekvence vyšší.

Obrázek 12: Originální obrázek (vlevo) a jeho diskrétní fourierova transformace (vpravo) – srovnáním s předchozím obrázkem pro „2D pulz“ lze „vidět“ obraz obou hlavních hran a jejich směrů a jejich zobrazení ve spektru

Na snímku je vidět, že ve spektru jsou výrazné tři „skupiny“ spektra pro jednotlivé hrany v originále. Směry spektra jsou kolmé na hrany. Spektrum má větší hodnoty kolem středu, směrem k větším hodnotám amplitudy klesají.

Jak zobrazovat frekvenční část FT

Jelikož při použití FT jedná o zobrazení (do) prostoru komplexních čísel, je obtížné toto zobrazit. Vzniká zde několik problémů, prvním je to, že výsledek je komplexní číslo, druhým problémem je, že spektrum má ss hodnotu v „rohu“. Třetím problémem je velký rozsah zobrazovaných hodnot. Pro základní náhled si zvolme obraz obdélníku – je vidět hlavní směry spektra (kolmé na hrany) a je patrný i pokles směrem k vyšších frekvencím.

Problém s komplexními čísly řešíme většinou tím, že nás fáze (až tak) nezajímá, takže používáme pouze amplitudu (modul). Zobrazujeme potom pouze tuto jednu hodnotu. Požadujeme-li zobrazení obou hodnot, potom nezobrazujeme komplexní čísla, ale stejně amplitudu a fázi. Můžeme se rozhodnout pro dva grafy, nebo pro jeden, kdy fázi a amplitudu „překryjeme“ a rozlišíme například pomocí barev – barevné kódování. Je možné zobrazit též Re a Im část zvlášť

Problém s tím, že po výpočtech je ss hodnota většinou v rohu vyřešíme přeskládáním obrázku tak, aby ss složka byla ve středu.

Zobrazení je možné tak jak je, s tím, že stejnosměrná složka je obvykle nejvyšší a tím je zbytek v zobrazení potlačen. Proto se upravuje logaritmováním před zobrazením. Problém s velkým rozsahem hodnot vyřešíme například tím, že před zobrazením hodnoty zlogaritmujeme.

různé způsoby zobrazování (frekvenční reprezentace, pouze amplituda) – vidíme zde zobrazení pomocí jasu, inverzní zobrazení pomocí jasu, zobrazení jasové kombinované s grafem v „řezu“, a 3D zobrazení grafu pomocí výškové mapy (hodnota = jas=výška)

prostorové uložení frekvencí se ss složkou v rohu, nebo ve středu

Obrázek 13: Originální obrázek (vlevo) a jeho diskrétní fourierova transformace (vpravo), je vidět, že obrázek je složitější oproti nenatočenému, je zde ale opět vidět hlavní směr hran a jim příslušné„vlnité plechy“

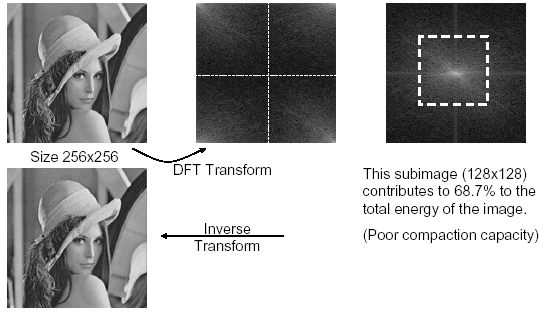
Obrázek 14: Diskrétní a zpětná FT – transformace je bezeztrátová. První frekvenční graf je nepřeskládaný, druhý je přeskládaný. Podle rozložení jasnějších oblastí je vidět, že i tato „tvarově pestrá“ předloha má více „energie“ v oblasti nižších frekvencí. V „prostřední“ čtvrtině je takřka 70% energie.

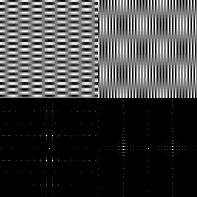
Obrázek 15: Spektra různých druhů obrázků. První obrázek demonstruje směry „vlnitých plechů“ a jejich obrazy (umístění odpovídá směru a frekvenci), druhý snímek demonstruje skládání spekter. Třetí snímek ukazuje spektra „znaků“ z nichž je opět patrné soustředění energie „ve středu“ a také že hlavní energie spektra jsou rozložena podél čar/hran/pulzů, které vyjadřují

základní vlastnosti

Je separabilní. Z pohledu na vzorec je zřejmé, že se dá 2D FT rozdělit na dvě postupné aplikace 1D FT (pro řádky a s výsledkem pro sloupce, nebo pro sloupce a poté pro řádku). Je vidět, že lze rozdělit na dva nezávislé integrály v jednotlivých směrech. Toto je dobře vidět na předchozích obrázcích „pulzu“. Na obrázku je vidět, že spektrum „kvádru“ je podobné jako spektrum 1D hrany. Ve druhém směru spektrum není – předloha se v tomto směru nemění (je konstantní, jak v prostorové doméně tak v 1D řezech spektra – proto je spektrum 2D pouze na ose (ss složky v daném směru)).

Platí princip superpozice. Linearita vůči sčítání a násobení konstantou v obou doménách.

Opět platí požadavek „rozšíření“ signálu do nekonečna pomocí opakování. Vznikne tak „periodický“ signál, který se dá vyjádřit diskrétním spektrem.

Pokud je v prostorové doméně tvar složen z několika hran, potom ve frekvenční doméně se objeví frekvence („pruhy“ v daném směru) pro tyto hrany.

Pro vyjádření 2D signálů se používá 2D frekvenční spektrum. Toto spektrum je symetrické podle počátku. Jedná se o bázi tvořenou sinusovým průběhem v jednom směru a konstantní hodnotu ve směru kolmém. Směr pruhů udává poloha ve frekvenční rovině. Vlastní hodnoty potom reprezentují fázi a amplitudu pruhů.

Čím jsou body dále od středu tím je frekvence vyšší.

ideální signál „typu“ vlnitý plech jak bylo uvedeno výše a jeho spektrum. Při „skutečném“ vyhodnocování je však signál většinou znehodnocen (změna jasu v ploše, zkreslení ...) takže výsledný signál není čistě harmonický, ale je sloučením celé řady signálů a proto nemůže být vyjádřen takto jednoduchým spektrem. Pokud máme v prostorové oblasti pravidelné pruhy, potom jsou obrazem dva body odpovídající frekvenci.

Není-li signál čistě periodický (například mírné jasové nebo geometrické zkreslení) potom se objeví vyšší harmonické (které se snaží kompenzovat nepřesnosti oproti „ideálnímu“ signálu)

Ve spektru tedy vznikají zázněje z důvodu kompenzeace jasu, zkreslení jasu, tvaru (jasové (vineting, pokles jasu ke kraji), geometrické) … opět vidíme, že problém ve FT – oko rozdíly v prostorové doméně nepostihne, ale ve FT je mírná změna kompenzována vyššími harmonickými, které mohou být dosti výrazné. Korekce (harmonické) mohou mít různá znaménka (jedna koriguje druhou …)

Pokud dojde k (mírné) tvarové deformaci (geometrické zkreslení), nebo k jasovému zkreslení (viněting), potom se objeví další vyjádřené frekvence v daném směru. Malá změna oproti ideálnímu průběhu může vést k výrazné změně v oblasti frekvenční.

Hodnocení „periodičnosti“ snímku podle viditelné části může být zrádné. Zatímco obraz vlevo na dalším snímku vypadá periodicky, z jeho frekvenčního spektra je patrné, že tato struktura není pravidelná ve smyslu (strojové) periodičnosti. Na rozdíl od toho v pravém snímku je vidět hlavní periodická složka, která je ovšem skrytá v „původním“ snímku, kde je mírně upravená ostatními signály

Obdobně lze vyjádřit i FT složitějších útvarů – například sledovat základní signál a jeho změny při natočení „hrany“ , natočení „obdélníku“, základ a natočení trojúhelníku (= součet odezev tří hran, který se dá vysledovat. Opět vidíme, že u vyšších frekvencí jsou nižší amplitudy.

v případě, že se objeví další odchylky (zde „schodovitost“ přímek) objeví se ve spektru další harmonické (korigující drobné odchylky vzniklé předchozími harmonickými)

Hodnocení „periodičnosti“ snímku podle viditelné části může být zrádné. Zatímco obraz vlevo vypadá periodicky, z jeho frekvenčního spektra je patrné, že tato struktura není pravidelná ve smyslu (strojové) periodičnosti. Na rozdíl od toho v pravém snímku je periodická složka, která je ovšem skrytá v „původním“ snímku

FT pruhu, čtverce, trojúhelníku a natočeného trojúhelníku

bod a jeho spektrum – čím užší je bod, tím širší je spektrum a naopak – je-li bod „ostrý“, potom spektrum má tvar sinc (zázněje)

FT složitějších útvarů – základ a natočení „hrany“ , natočení „obdélníku“, základ a natočení trojúhelníku (= součet odezev tří hran, který se dá vysledovat. Opět u vyšších frekvencí nižší amplitudy. „vyfiltrování“ určitého směru hran – maska frekvencí, které se na tom podílejí – odstranění frekvencí pro ostatní směry.

Zpětná transformaca a vliv ořezání spektra na kvalitu – úvod do filtrů

Obraz obdélníku a vliv omezení spektra na rekonstrukci vidíme na následujícím příkladu.

Základem je obdélník a jeho obraz ve FT. Všimněte si dvou hlavních směrů spektra v transformaci, které respektují natočení obdélníku. Ve středu je stejnosměrná složka, která udává ss posunutí (střední „výška“ obrazu). Směrem ke kraji se zvětšují frekvence, a je zde patrné i snižování amplitudy pro tyto vyšší frekvence (v nižších frekvencích je více „energie“). Nižší frekvence respektují/vytvářejí základní tvar, vyšší frekvence popisují ostré přechody (hrany). Jednotlivé frekvence se doplňují/skládají - žádná z obsažených frekvencí (pro běžný snímek) není „zázračná“ = nepostihuje zásadním způsobem prostorovou scénu.

snímek ukazuje původní spektrum a spektra frekvenčně „ořezaná“ (dá se představit i tak, že došlo k aplikaci filtru). V prostřední řadě jsou potom jasové „originály“ k příslušným spektrům. Na nich je vidět, že čím širší spektrum se použije, tím je obraz „lepší“ (méně promodulovaný a strmější hrany). Dále je vidět, že „ostré ořezání“ spektra vede k záznějům. Tyto zázněje mohou zvyšovat kontrast na hranách.

čtverec originál je tvar s ostrými hranami, který převedeme do FT. Ve FT vezmeme čtvercovou část spektra od středu a z této části uděláme IFT. Výsledkem je „rozmazený“ obrázek, který je tím ostřejší/lepší, čím širší oblast vezmeme. Všímněme si překmitů a „podkmitů“ u hran (které se dají využít pro zvýšení kontrastu, ale způsobují zhoršení lineární části) – tyto „ořezání“ frekvencí lze považovat za způsobené dolnofrekvenčními filtry s různými frekvencemi (zlomu frekvenční charakteristiky).

Pokud ve frekvenční doméně vybereme pouze oblast kolem středu, dojde k rozmazání hran a rozkmitání zbytku. „Ostré“ filtry ve frekvenční doméně jsou nevhodné, protože výsledek je rozkmitán. Výhodnější je postupné „upadání“ frekvencí na hranách filtrů (butterworth, gauss). čím více frekvencí použijeme, tím lepší průběh dostaneme při inverzní transformaci.

Tvorba filtrů by měla vycházet z postupného (hladšího) průběhu filtrů ve frekvenční oblasti – gauss, spacek, canny, bessel… Odstraňování šumu. nevhodnost – „ostrých“ filtrů známých z časové domény, kde jsou snadno spočítatelné – ve FT „šumí-kmitá“ – nerovnoměrné odstranění frekvencí díky sync. Tvar sinc je nevhodný proto, že některé frekvence „přeskakuje“ - například u dolní propusti frekvence za prvním minimem mají větší hodnotu než toto minimum a tedy na tvorbě výsledného signálu se podílí i vyšší frekvence než frekvence potlačené. Tyto nízké hodnoty jsou problémem i při použití při inverzní filtraci, kdy se s nimi dělí, což (při dělení nulou ale i malými hodnotami) způsobuje problémy. Proto lépe odstranit postupně / plynule.

testovací vzor – siemensova hvězdice – vhodný pro testování – obsahuje různé směry hran i různé frekvence

aplikace filtrů dolno- a horno- frekvenčních na siemensovu hvězdici (vlevo jsou nízké frekvence vypuštěny, vpravo jsou vypuštěny vysoké)

FT je možné použít i k „vyfiltrování“ určitého směru hran – maska frekvencí, které se na tom podílejí – odstranění frekvencí pro ostatní směry. Zde je příklad, kdy se vyberou střední frekvence (pásmová propust) v daném směru. Po IFT je vidět, že došlo potlačení určitých směrů a ve zbytku jsou nejvěrněji vykreslené středy čar (střed a kraj, tedy vysoké a nízké frekvence jsou také zobrazeny hůře.)

vlevo je vidět ponechaná část spektra. Vpravo zpětná transformace. Je vidět, že jsou ponechány střední frekvence ve směru kolmém na směr který určují ponechané oblasti spektra. Je zde tedy použit filtr směrový středněfrekvenční.

FT různých znaků a tvarů

ukázka různých znaků a jejich obrazy. Je patrné, že spektrum obsahuje vzor „kolmý“ na nejvýznamější přímky v originále

FT písmenek fontů – E, Z, X, kolečko, půlkolečko, hvězdička … - všimněme si jak je to tvořeno z obrazů hran – vyjádření dominantních směrů vyjadřujících vyjádřené hrany. písmena S, O – symetrie, více frekvencí – není hlavní směr čar

filtry a filtrace

Lineární filtrace integrálními transformacemi se nejčastěji používá pro potlačení šumu, zvýraznění hran a odstranění strukturovaného šumu dobře odlišitelného od signálu ve frekvenčním spektru. Filtrace je realizována pomocí pomocí konvolutorních filtrů. Jelikož realizace (vlastní) konvoluce je ve frekvenční oblasti snadnější, je výhodné ji realizovat zde. Fourierova transformace umožňuje interpretovat metody předzpracování obrazu založené na konvoluci jako filtraci ve frekvenční oblasti. Většinou je ovšem „reálný“ snímek (a případně i filtr) nutno převést do frekvenční oblasti a zpět – tato operace nám využití frekvenční oblasti „prodraží“ a musíme tedy zvážit, zda celkové „náklady“ jsou výhodné. Dá se říci, že v prostorové doméně je výhodné realizovat menší a jenodušší filtry (takové, které mají málo výpočtů, nebo je lze optimalizovat). Též filtry nelineární (vůči FT) je nutné provádět v prostorové doméně. Ve frekvenční doméně je výhodné realizovat (tvarově) složité a větší filtry.

Společně s vhodností různých filtrů pro různé domény je nutné říci, že filtry pro obě domény je lépe konstruovat rozdílně. Zatímco v prostorové doméně jsou výpočetně výhodné a nejčastěji používané filtry s „ostrými“ hranami, ve frekvenční doméně jsou to „hladké“ filtry. „ostré“ filtry jsou ve frekvenční doméně nevhodné, protože nevýhodou je, že odezva je typu sinc, což znamená, že frekvence neklesají (resp. Nestoupají) monotónně (útlum frekvencí není plynulý ale frekvence „dále“ mají vyšší váhu než předchozí). Nevýhodou tohoto je i při využití v inversní filtraci, že při dělení těmito nízkými hodnotami vzniká chyba ve výsledku. Nevýhodat „hladkých“ filtrů v časové oblasti je jejich velká výpočetní náročnost.

Filtry v FT jsou nejčastěji realizovány na bázi podobnosti s gaussovou křivkou. Tyto filtry jsou „rozmazávací“. Gaussovou křivkou se aproximuje také „rozložení“ paprsku na optice. Nebo-li předpokládáme, že se procházející kvalitní (ostře ohraničený) paprsek při průchodu optickou soustavou „rozostřuje“ vlivem prostředí. Pro modelování tohoto jevu se používá gaussova křivka. Jedná se vlastně o „filtr“, který je nechtěný, parazitní a který je tvořen prostředím, kterým pořizujeme snímky. V přesnějších modelech je nutné z jeho vlivem počítat. K tomu musíme mít možnost stanovit jeho model identifikovat velikost jeho parametrů. Na základě stanovení modelu a parametrů můžeme provádět i korekce obrazu.

Filtry v image procesingu mohou být „symetrické“ kolem středu. Na rozdíl od zpracování časových signálů, kdy není možné pracovat se vzorky, které teprve přijdou, je zde možné použít kompletní okolí pro výpočet výsledné hodnoty. V obrázku známe celé okolí a tedy můžeme mít filtr symetrický k místu, pro které výsledek počítáme. Výhodou tedy je, že lze udělat i derivaci v daném místě (jsou známy hodnoty na obou stranách).

Z obrazu jednotkového skoku je patrné, že je jím sinc, který v sobě obsahuje „celé“ (=široké) spektrum. Proto jsou filtry aplikované v prostorové doméně (s ostrými hranami) nevhodné. Filtry ve frekvenční oblasti by měly omezovat frekvenční spektrum tak aby „ořezávaly“ frekvence „větší než“. Opět se nedoporučuje ostrý skok (z důvodu, že zpětná transformace je opět sinc). Přechod z „propustné“ do „nepropustné“ části frekvencí je lepší volit plynulý. Často se používá signál, který je variací na gaussovu křivku (gauss, laplace, spacek, canny … Inverzní funkce je podobná funkci originální). Popřípadě čebyšev …

Návrh těchto filtrů umožňuje splnit požadavky na odstranění šumu, kvalitní umístění hrany i odstranit vícenásobné odezvy (maxima ve výstupu filtru) v oblasti hrany.

„pravoúhlý“ filtr je špatně i proto, že jeho odezva ve frekvenčním spektru je sinc. Nevýhodou jsou zejména frekvence, ve kterých jsou minima. Pokud tato minima jsou nulová („trefí“ se počet vzorků a délka filtru do správného poměru), potom se s tímto filtrem nedá pracovat v situacích, kdy je nutná například inverzní filtrace.

Filtry hranové potom odvozujeme od těchto filtrů jako jejich derivaci. Z náhledu je zřejmé, že se u těchto hranových filtrů nejedná o filtry vysokofrekvenční jak by se dalo očekávat u hranových detektorů, ale o filtry středněfrekvenční. Použití středněfrekvenčních filtrů je kompromisem mezi zvýrazněním hrany (potlačením ss složek) a eliminací šumu. Při použití pouze vysokofrekvenční složky by došlo ke zvýraznění signálů s vysokými frekvencemi, kterými je (bohužel) často aditivní šum připojený ke snímku. Jelikož požadujeme u filtrů invariantnost vůči šumu, je nutné vysoké frekvence potlačit i za cenu toho, že maxima hranového filtru nebudou kvalitní (ostrá, výrazná).

Předpokládejme opět, že f je vstupní obraz a F výsledek fouriérovy transformace. Konvoluční filtr h lze vyjádřit jako jeho Fourierův obraz H. Matici h můžeme nazývat odezvou bodového zdroje (impulsní charakteristikou filtru) a matici H frekvenční charakteristikou filtru. Zda pro filtraci použijeme h nebo H je z teoretického hlediska lhostejné (musíme tak ovšem činit ve správné doméně). V prvním případě pracujeme v prostorové oblasti ( dvojrozměrná analogie časové oblasti pro jednorozměrné průběhy) a ve druhém případě ve frekvenční.

Nyní pro názornost ukážeme jednoduché příklady dvojrozměrné filtrace ve frekvenční oblasti. Jde o dvojrozměrné případy frekvenčně selektivních filtrů.

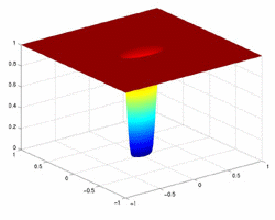
Dolní propust: odpovídá frekvenční charakteristice filtru H (u,v) s malými hodnotami v místech hodně vzdálených od počátku (malé zesílení pro vysoké frekvence) a velkými hodnotami blízko počátku, viz. obr. Filtr přenese nízké frekvence a potlačí vysoké frekvence. Chová se jako filtrace průměrováním v prostorové oblasti, tedy rozmazává ostré hrany.

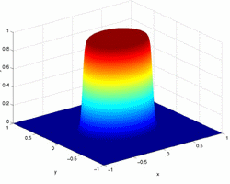
Obrázek 1: Dolní propust

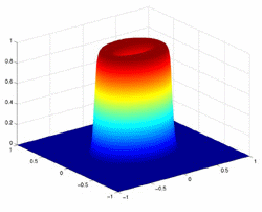
Horní propust: odpovídá frekvenční charakteristice filtru H (u,v) s malým zesílením blízko počátku a velkým zesílením v oblasti vysokých frekvencí, tj. dále od počátku, viz obr.2. Jelikož filtr propouští pouze vyšší frekvence, jsou potlačeny ss plochy a zvýrazněny oblasti přechodů. Jelikož je filtr symetrický, dojde ke zvýraznění hran všech směrů.

Obrázek 2: Horní propust

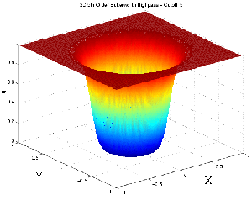
Pásmová propust: propustí jen frekvence v určitém pásmu, viz. obr. Podobně jsou konstruovány filtry, které propustí jen signály o určitém směru, tj. fázi, řečeno terminologií Fouriérovy transformace. Tento filtr je nejpoužívanějším „hranovým“ filtrem, protože zvýrazní „větší“ hrany, zatímco potlačí šum, který má většinou vysoké frekvence a tvoří „škodlivý“ signál. Jedná se tedy o kompromisní kombinaci horní (zvýraznění hran) a dolní (potlačení šumu) propusti.

Obrázek 3: Pásmová propust

Pro tvorbu filtrů není tedy dobré „ořezat“ frekvence přímo (funkcí ano/ne), protože by v prostorové oblasti došlo k záznějům a tedy odpovídající tvar by byl hrana a v jejím okolí zázněje. Lepší je vytvořit přechod ano/ne filtru pomocí S křivky, gaussovy křivky, butterworth…, Výhodnější je tedy postupné „upadání“ frekvencí na hranách filtrů (které zaručují butterworth, gauss...). Čím více frekvencí použijeme, tím lepší průběh dostaneme při inverzní transformaci.

příklad filtrace. Vlevo je snímek a jeho spektrum. Uprostřed je „rozmazávací“ filtr a jeho spektrum. Vpravo je konvoluce levých dvou obrázků (snímek a filtr) a dole příslušné spektrum, které je násobkem předchozích dvou spekter (pro příslušné pozice „nad sebou“). Je zde také vidět, že filtr je široký, zatímce jeho spektrum „úzké“. V prostorové doméně tedy dojde ke značnému rozostření, zatímco ve frekvenční doméně zůstane pouze oblast v okolí nejnižších frekvenc

Filtrace originálního obrazu „rozmazávacím“filtrem gaussova typu. Srovnání výpočetní náročnosti. Pro obraz s rozměry MxN a filtr s rozměry PxQ je výpočetní náročnost v prostorové doméně VNP = 2*(M-P)*(N-Q) * P*Q (neboli každý výsledný prvek, kterých je díky velikosti filtru méně, je vytvořen s výpočtů nad plochou filtru. Pokud předpokládáme, že dojde k násobení a potom sečtení, jsou potřebné vždy dvě operace). Vlastní FT spotřebuje M*N výpočtů (násobení komplexních čísel). K tomu musíme připočítat dva převody obrázků (obrázek a filtr) a dvě transformace (přímá a inverzní) – takže 4x FT pro pole rozměrů M*N. V případě, že je možné využít FFT, potom výpočetní náročnost klesá.

Existuje celá řada filtrů (Canny, Spacek, ...), které mají jako základ funkci typu gauss, liší se však svými parametry (pomocí nastavení parametrů můžeme ovlivňovat kvalitu filtru z hlediska potlačení šumu, rozmazání hrany, jedinečnosti odezvy ... Tyto filtry se liší tím jakou váhu dávají jednotlivým z těchto požadavků – protože požadavky působí proti sobě je nutné zvolit určitý kompromis).

antialiasing – u diskrétních signálů se nás netýká při převodu FT, protože tu volíme tak, aby byla bezeztrátová. Dochází k němu především na úrovni optické soustavy, nebo pomocí „rozmazávacích“ filtrů. Někdy se zavádí antialiasing filtry.

zpracování signálu – použití FT - konvoluce, korelace, filtrace

Ke zpracování signálů pomocí FT se používá konvoluce (realizované pomocí násobení spekter) za použití filtrů. V případě, kdy potřebujeme některou vlastnost zvýraznit, používáme filtraci filtrem s danou vlastností. V případě, kdy potřebujeme vlastnost potlačit můžeme použít filtr s jehož aplikací potlačíme danou vlastnost, nebo můžeme použít inverzní filtraci.

Za pomocí vhodně navržených filtrů můžeme například zvýraznit (ponechat) nebo potlačit (rozmazat) hrany daného směru. V případě, že je potřebné hrany „zaostřit“ (při jejich rozmazání pohybem, nebo špatným zaostřením) potom použijeme inverzní filtrace s filtrem, který je modelem „nechtěného“ působení, které chceme odstranit.

Je-li v obraze periodické rušení (např. mřížka), potom se projeví ve spektru jako několik bodů, které v případě, že je odstraníme, dopomohou k tomu, že periodické rušení zmizí po zpětné transformaci z obrazu. Musí ovšem platit, že rušení je na dané frekvenci výraznější než originál. Má-li originální užitečná hodnota srovnatelnou hodnotu jako obraz šumu, potom odstraněním vznikne chyba opačná. Lépe je proto například použít medián, který danou oblast nevynuluje, ale pouze „přizpůsobí“ okolním hodnotám. Pro lepší činnost je samozřejmě výhodou, dokážeme-li z něčeho určit typ rušení a jeho parametry.

zašuměnný signál a jeho spektrum – jsou zde vidět vrcholy značící periodicitu. V prostorové doméně není periodicita výrazně viditelná.

výsledný signál po inverzní filtraci oblastí odpovídajícch periodické struktuře

opačný případ. V původním signálu byla periodicita (vzniklá při tisku samotným tiskem nebo podkladem). Nyní je tedy nutné maxima vzniklá periodickým signálem odstranit

Je také možné převést do spektra tvar objektu který hledáme a pomocí jeho násobení (konvoluce) se spektrem obrázku hledat v obrázku tento tvar. filtr na hledání znaku v textu (=složitý tvar)

Šum obvykle mívá široké frekvenční pásmo, a proto ho potlačí, když jsou omezeny (odstraněny) vysoké frekvence dolní propustí, viz obr. 5. Naneštěstí spolu se šumem mizí všechny jevy v obrázku odpovídající vysokým frekvencím (hrany, detaily jako tenké čáry,atd.). Obrázek je proto celkově rozmazán.

Obrázek 4: Originální obraz

Obrázek 5: Dolní propust

Hrany odpovídají místům kde se náhle mění obrazová funkce, což přispívá k vysokým frekvencím ve spektru. Pokud vyšší frekvence relativně zesílíme, a to udělá horní propust, zvýrazní se v obrazu hrany viz obr. 6.

Obrázek 6: Horní propust

Vytvoříme-li si obraz daného posunu – přímky, můžeme s jeho pomocí – znalost zkreslení – vytvořit odhad nezkresleného obrazu. Zkresleni = Filtr.Original.

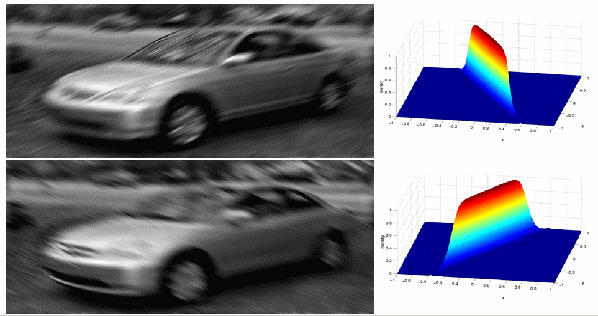
Obrázek 7: Obrázek auta filtrovaný dolní propustí Butterworthovým filtrem – frekvence řezu je 0.03 ve směru hlavní osy a 0.75 ve směru vedlejší osy, rotace je 60 º pro horní obrázek pro spodní je rotace 120 º.

Jiný snímek rozmazaný pohybem a jeho spektrum, ze kterého je patrné, že ve snímku došlo k nějaké závislost a kterým směrem

obraz znázorňující pohyb předchozího snímku. Je možné ho též považovat za filtr, který byl uplatněn na původní obrázek. Lze též postupovat tak, že se z předchozího spektra vezme pravidelná struktura a stou se provede zpětná transformace

výsledný „doostřený“ snímek. Inverzní filtrace

Obrázek 8: Obrázek auta filtrovaný horní propustí (Butterworthův filtr pátého řádu)

Obrázek 9: Filtr typu horní propust použitý při filtraci obrázku auta

Obrázek 10: Obrázek auta filtrovaný dolní propustí (Butterworthův filtr 27 řádu)

Obrázek 11: Filtr typu dolní propust použitý při filtraci obrázku auta

astigmatizmus a jeho zjištění ze spektra – zastoupení frekvencí nerovnoměrné – zjištění spektra ke kvalitě zaostření

Na snímku je vidět vliv rozmazání na spektrum. Ostrý obraz má širší spektrum, protože k jeho vyjádření jsou nutné vyšší frekvence. Čím „širší“ je centrální části, tím více frekvencí je zastoupeno a tím je obraz ostřejší (zaostřenější). Je možné určit též astigmatizmus – rozdílné rozmazání v každém směru. Astigmatizmus a jeho zjištění ze spektra je tedy možné na základě zastoupení frekvencí v jednotlivých směrech. Podle zastoupení frekvencí můžeme určit kvalitu zaostření původního obrazu - využívá se například při skenování filmů.

Testovací obrazce – například siemensova hvězdice – všechny frekvence ve všech směrech.

FFT – výpočty, programování

postupné řešení – z pohledu na vzorec 2D transformace je vidět, že lze vyřešit jako postupnou aplikaci jednorozměrných (nejprve na sloupce a s výsledkem řádkově). Je vidět, že lze rozdělit na dva nezávislé integrály v jednotlivých směrech. Na obrázku je vidět, že spektrum „kvádru“ je podobné jako spektrum 1D hrany. Ve druhém směru spektrum není – předloha se v tomto směru nemění (je konstantní, jak v prostorové doméně tak v 1D řezech spektra – proto je spektrum 2D pouze na ose (ss složky v daném směru)). Na tom, který směr se počítá první nezáleží.

Pro vlastní výpočet se využívají stejné algoritmy jako pro 1D kde základem pro výpočet jsou řádky nebo sloupce. Je možné pracovat s polem libovolného rozměru. Pokud chceme provádět výpočty rychleji, musíme použít algoritmy FFT a to znamená, že pole musí mít rozměry rovné mocninám dvou (nemusí být oba rozměry stejné). Můžeme použít i zjednodušení pro současný výpočet sitnálu a filtru.

Nezapomínejme na periodické doplnění signálů při FT. To zanmená, že filtr na okrajích zasahuje „na druhou stranu“. Tyto přesahy musíme vyřešit – budťo rozšířením signálu o „prázdné“ kraje, nebo vypuštěním „přesahů“ z výsledku. V případě, že signál doplňujeme na krajích, neměli bychom to dělat „ostře“. Doplňování provádíme z důvodu rozšíření na mocninu dvou, nebo z důvodu odstranění ovlivnění krajních částí signálu díky přesahům filtru.

Poznámky

FT existuje i v polárních a sférických souřadnicích

Literatura

diskrétní FT http://apfyz.upol.cz/ucebnice/down/mini/fourtrans.pdf

transformace obrazu http://uprt.vscht.cz/mudrova/zob/prednasky/06-FOURIER/fouriercz.pdf

FT http://www.cs.unm.edu/~brayer/vision/fourier.html

Frekvenční filtrace DFT http://www.owlnet.rice.edu/~elec301/Projects01/image_filt transform.html

DFT http://www.kiv.zcu.cz/~novyp/aos/dft.pps

FT http://www.inforum.cz/inforum2001/prispevky/psohlavec.htm

John C. Russ, The Image Processing Handbook, 4th Edition, CRC Press, 2002, ISBN 0-8493-1142-4

last modification 2009-09-25